Ejercicio 31.
Sea ![]() un número real. Encontrar todas las funciones continuas
un número real. Encontrar todas las funciones continuas ![]() tales que
tales que ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Como ![]() es continua en
es continua en ![]() , tenemos que
, tenemos que ![]() es continua en
es continua en ![]() , por lo que
, por lo que ![]() es derivable en
es derivable en ![]() por el teorema fundamental del Cálculo, y entonces
por el teorema fundamental del Cálculo, y entonces ![]() es derivable en
es derivable en ![]() (ya que es igual a
(ya que es igual a ![]() ).
).
Por tanto, si derivamos a los dos lados de ![]() , llegamos a
, llegamos a 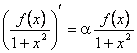 y entonces
y entonces ![]() , por lo que
, por lo que ![]()
Pero si sustituimos ![]() por 0 en la ecuación inicial, tenemos que
por 0 en la ecuación inicial, tenemos que ![]() . Sustituyendo ahora
. Sustituyendo ahora ![]() por 0 en las funciones obtenidas, tenemos que
por 0 en las funciones obtenidas, tenemos que ![]() , luego la solución es
, luego la solución es ![]() .
.
Ejercicio 32.
Sean ![]() ,
, ![]() dos polinomios primos relativos con raíces
dos polinomios primos relativos con raíces ![]() , …,
, …, ![]() y
y ![]() , …,
, …, ![]() respectivamente. Probar que
respectivamente. Probar que ![]() es un entero y determinar su valor
es un entero y determinar su valor
(Propuesto por José Luís Díaz Barrero)
Solución
Como ![]() ,
, ![]() son primos relativos no tienen ninguna raíz común, por lo que
son primos relativos no tienen ninguna raíz común, por lo que ![]() , y entonces la expresión
, y entonces la expresión ![]() está bien definida.
está bien definida.
Si factorizamos ahora ![]() ,
, ![]() , obtenemos
, obtenemos ![]() ,
, ![]() , luego
, luego

(El signo ![]() es porque hay
es porque hay ![]() factores de la forma
factores de la forma ![]() : Tenemos
: Tenemos ![]() factores
factores ![]() ,...,
,..., ![]() , ..., y tenemos
, ..., y tenemos ![]() factores
factores ![]() ,...,
,..., ![]() )
)
Observación
El resultado se puede generalizar a:
Sean ![]() ,
, ![]() dos polinomios con raíces
dos polinomios con raíces ![]() , …,
, …, ![]() y
y ![]() , …,
, …, ![]() respectivamente, y sin raíces comunes. Entonces
respectivamente, y sin raíces comunes. Entonces ![]()
Ejercicio 33.
Sea ![]() la descomposición en factores primos de un natural
la descomposición en factores primos de un natural ![]() tal que la suma de sus divisores es
tal que la suma de sus divisores es ![]() . Probar que
. Probar que 
(Propuesto por José Luís Díaz Barrero)
Solución
Si llamamos ![]() a la suma de los divisores de
a la suma de los divisores de ![]() , se sabe que:
, se sabe que:
![]() , luego se puede escribir la condición como
, luego se puede escribir la condición como ![]()
Entonces, si multiplicamos por ![]() a los dos lados de la primera desigualdad que hay que probar, ésta queda:
a los dos lados de la primera desigualdad que hay que probar, ésta queda:
![]()
Esto equivale a ![]() , es decir,
, es decir, ![]()
Pero esta última desigualdad es cierta al ser ![]() (ya que
(ya que ![]() ).
).
Si multiplicamos ahora por ![]() a los dos lados de la segunda desigualdad que hay que probar, ésta queda:
a los dos lados de la segunda desigualdad que hay que probar, ésta queda:
![]() .
.
Esto equivale a ![]() . Pero esta última desigualdad es cierta al ser
. Pero esta última desigualdad es cierta al ser ![]()
Observaciones
1) El menor número que cumple la condición del enunciado es 154345556085770649600
2) Sólo se conocen 245 números que cumplan dicha condición. Se conjetura que no hay más.
Ejercicio 34.
Sean ![]() matrices del mismo orden. Probar que
matrices del mismo orden. Probar que ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Suponemos que ![]() son matrices cuadradas de orden
son matrices cuadradas de orden ![]() .
.
Entonces, haciendo ![]() , donde
, donde ![]() es la i-ésima columna de
es la i-ésima columna de ![]() , llegamos a
, llegamos a ![]() .
.
Si hacemos ahora ![]() , donde
, donde ![]() es la i-ésima fila de la última matriz, obtenemos
es la i-ésima fila de la última matriz, obtenemos ![]() , donde
, donde ![]() es la matriz nula de orden
es la matriz nula de orden ![]() .
.
Por tanto ![]()
Ejercicio 35.
Sea ![]() una función continua. Calcular
una función continua. Calcular ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Como ![]() es una función continua, para todo
es una función continua, para todo ![]() hay un polinomio
hay un polinomio ![]() tal que
tal que ![]() para todo
para todo ![]() (teorema de Stone-Weierstrass). Pero como
(teorema de Stone-Weierstrass). Pero como ![]() es un polinomio, su serie de Fourier en
es un polinomio, su serie de Fourier en ![]() converge uniformemente a
converge uniformemente a ![]() , por lo que existe un número
, por lo que existe un número ![]() tal que
tal que ![]() para todo
para todo ![]() , donde
, donde ![]() es la
es la ![]() truncación de la serie de Fourier de
truncación de la serie de Fourier de ![]() .
.
Por tanto, ![]() para todo
para todo ![]() , y entonces
, y entonces
![]() (hemos aplicado la identidad
(hemos aplicado la identidad ![]() en las dos desigualdades).
en las dos desigualdades).
Tenemos por tanto que:
![]() , es decir:
, es decir:
![]() . Esto es equivalente a:
. Esto es equivalente a:
![]()
Ahora, tenemos que 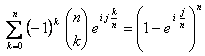 , donde
, donde ![]() es la unidad imaginaria. Entonces, como
es la unidad imaginaria. Entonces, como ![]() cuando
cuando ![]() , llegamos a:
, llegamos a:
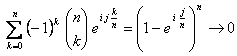 cuando
cuando ![]() para todo
para todo ![]() .
.
Pero al ser ![]() , tenemos que
, tenemos que ![]() ,
, ![]() cuando
cuando ![]() para todo
para todo ![]() , y así:
, y así:
![]() cuando
cuando ![]() . Esto implica que
. Esto implica que ![]() cuando
cuando ![]() para todo
para todo ![]() , y así:
, y así:
![]() cuando
cuando ![]() .
.
Tenemos por tanto que ![]() , por lo que
, por lo que ![]() para todo
para todo ![]() y entonces:
y entonces:
![]() . De la misma forma se puede ver que
. De la misma forma se puede ver que ![]() .
.
Como consecuencia, ![]()
Ejercicio 36.
Sea ![]() el n-ésimo número de Fibonacci. Probar que
el n-ésimo número de Fibonacci. Probar que ![]() no puede ser expresado como producto de dos números de Fibonacci mayores que 1
no puede ser expresado como producto de dos números de Fibonacci mayores que 1
(Propuesto por José Luís Díaz Barrero)
Solución
Vemos primero que ![]() si
si ![]() y
y ![]() , suponiendo que
, suponiendo que ![]() es el mínimo entre
es el mínimo entre ![]() :
:
Para verlo, expresamos ![]() de forma explícita como
de forma explícita como ![]() , donde
, donde ![]()
Por tanto, si ![]() tenemos que
tenemos que
![]() si y sólo si
si y sólo si
![]()
Pero el lado izquierdo de esta desigualdad es mayor ó igual que

(ya que

y todos los exponentes de ![]() en el lado derecho de la desigualdad son mayores que
en el lado derecho de la desigualdad son mayores que ![]() ).
).
Ahora,  es positivo si y sólo si
es positivo si y sólo si 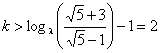 (ya que
(ya que ![]() ).
).
Por tanto, si ![]() ,
, ![]() en este caso.
en este caso.
Si ![]() tenemos que
tenemos que
![]() si y sólo si
si y sólo si
![]()
Pero el lado izquierdo de esta desigualdad es mayor ó igual que
 (ya que
(ya que
 y todos los exponentes de
y todos los exponentes de ![]() en el lado derecho de la desigualdad son mayores ó iguales que
en el lado derecho de la desigualdad son mayores ó iguales que ![]() ). Ahora,
). Ahora, ![]() es positivo si y sólo si
es positivo si y sólo si 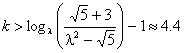 .
.
Por tanto, si ![]() ,
, ![]() en este caso. Pero para
en este caso. Pero para ![]() tenemos que
tenemos que ![]() , y por tanto
, y por tanto ![]() . Entonces, si
. Entonces, si ![]() , como
, como ![]() , llegamos a que
, llegamos a que ![]() , contradicción con que
, contradicción con que ![]() es estrictamente creciente si
es estrictamente creciente si ![]() . Para
. Para ![]() tenemos que
tenemos que ![]() , y por tanto
, y por tanto ![]() ó
ó ![]() . Entonces, si
. Entonces, si ![]() , como
, como ![]() , llegamos a que
, llegamos a que ![]() , contradicción con que
, contradicción con que ![]() es creciente. Si
es creciente. Si ![]() , como
, como ![]() , llegamos a que
, llegamos a que ![]() y entonces
y entonces ![]() , contradicción con que
, contradicción con que ![]() es estrictamente creciente si
es estrictamente creciente si ![]() . Por tanto,
. Por tanto, ![]() si
si ![]() .
.
Si ![]() tenemos que
tenemos que
![]() si y sólo si
si y sólo si
![]()
Pero el lado izquierdo de esta desigualdad es mayor ó igual que
![]() (ya que
(ya que
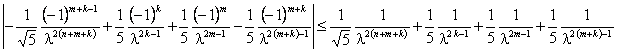 y todos los exponentes de
y todos los exponentes de ![]() en el lado derecho de la desigualdad son mayores ó iguales que
en el lado derecho de la desigualdad son mayores ó iguales que ![]() ). Ahora,
). Ahora, ![]() es positivo si y sólo si
es positivo si y sólo si  . Por tanto, si
. Por tanto, si ![]() ,
, ![]() en este caso.
en este caso.
Entonces, si ![]() con
con ![]() , será
, será ![]() , y por tanto
, y por tanto ![]() . Podemos además suponer sin pérdida de generalidad que
. Podemos además suponer sin pérdida de generalidad que ![]() . Por lo visto anteriormente, esto implica que
. Por lo visto anteriormente, esto implica que ![]() , luego
, luego ![]() , contradicción. Por consiguiente,
, contradicción. Por consiguiente, ![]() no puede ser expresado como producto de dos números de Fibonacci
no puede ser expresado como producto de dos números de Fibonacci ![]() , con
, con ![]()
Ejercicio 37.
Calcular el ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Se cumple que 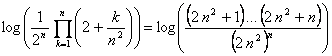
Vemos ahora que ![]() para todo
para todo ![]() . Para ver esto, probamos primero que:
. Para ver esto, probamos primero que:
![]() para
para ![]() , donde
, donde ![]() es la parte entera. Esta desigualdad equivale a:
es la parte entera. Esta desigualdad equivale a:
![]() , es decir,
, es decir, ![]() .
.
Pero como la función ![]() es creciente si
es creciente si ![]() , tenemos que el mínimo de
, tenemos que el mínimo de ![]() con
con ![]() se alcanza para
se alcanza para ![]() , por lo que:
, por lo que:
![]() (al ser
(al ser ![]() )
)
Esto implica que:
![]() si
si ![]() es par, y:
es par, y:
![]() si
si ![]() es impar, por lo que
es impar, por lo que
![]() en cualquier caso.
en cualquier caso.
Vemos ahora que ![]() para
para ![]() . Esta desigualdad equivale a:
. Esta desigualdad equivale a:
![]() , es decir:
, es decir:
![]() . Pero como el máximo de la función
. Pero como el máximo de la función ![]() se alcanza en
se alcanza en ![]() , tenemos que
, tenemos que
![]() como queríamos.
como queríamos.
Esto implica que:
![]() si
si ![]() es par, y:
es par, y:
![]() si
si ![]() es impar, por lo que
es impar, por lo que
![]() en cualquier caso.
en cualquier caso.
Tenemos entonces que:
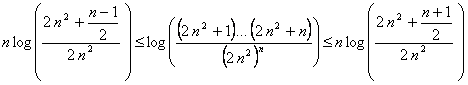 , con
, con 
(hemos aplicado la equivalencia ![]() si
si ![]() en la primera igualdad).
en la primera igualdad).
Por tanto, 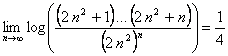 (Sandwich), con lo que
(Sandwich), con lo que ![]()
Ejercicio 38.
Sea n un entero positivo. Probar que:
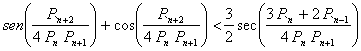 , donde
, donde ![]() es el n número de Pell, definido por
es el n número de Pell, definido por ![]() ,
, ![]() y para
y para ![]() ,
, ![]()
(Propuesto por José Luís Díaz Barrero)
Solución
Tenemos que ![]() para todo n, como se puede ver fácilmente por inducción, por lo que
para todo n, como se puede ver fácilmente por inducción, por lo que ![]() ,
, ![]() .
.
Tenemos además que ![]() ,
, ![]()
(En la primera desigualdad hemos aplicado que ![]() es una sucesión creciente: Para
es una sucesión creciente: Para ![]() ,
, ![]() , y
, y ![]() ).
).
Tenemos por tanto ![]() y
y ![]() para todo n. De estas últimas desigualdades obtenemos que
para todo n. De estas últimas desigualdades obtenemos que  , por lo que basta con probar que
, por lo que basta con probar que 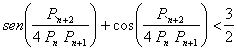 . Para ello, es suficiente con probar que
. Para ello, es suficiente con probar que ![]() para todo
para todo ![]() .
.
Pero en ![]() tenemos que
tenemos que ![]() , con
, con ![]() .
.
Tenemos también que ![]() , por lo que el máximo de
, por lo que el máximo de ![]() en
en ![]() es
es ![]() y entonces:
y entonces:
![]() como queríamos.
como queríamos.
Ejercicio 39.
Sea n un número natural y f una función convexa. Probar que 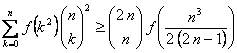
(Propuesto por José Luís Díaz Barrero)
Solución
La desigualdad es equivalente a  . El lado izquierdo de esta desigualdad es una combinación lineal de valores de f.
. El lado izquierdo de esta desigualdad es una combinación lineal de valores de f.
Veamos que la suma de los coeficientes es 1, es decir, que 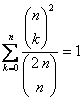 , o equivalentemente, que
, o equivalentemente, que  :
:

(Por cada forma de tomar k elementos de los n primeros, hay ![]() formas de tomar
formas de tomar ![]() elementos de los n últimos, luego el número de formas de tomar k elementos de los n primeros y
elementos de los n últimos, luego el número de formas de tomar k elementos de los n primeros y ![]() elementos de los n últimos es:
elementos de los n últimos es: ![]() . Esto nos lleva a la tercera igualdad. La identidad
. Esto nos lleva a la tercera igualdad. La identidad ![]() implica la última igualdad).
implica la última igualdad).
Por tanto, como f es convexa, podemos aplicar la desigualdad de Jensen y entonces  .
.
Por otro lado, es conocida la igualdad en números combinatorios  . Vamos a ver que
. Vamos a ver que ![]() :
:
![]() , siendo esta última igualdad cierta para todo n.
, siendo esta última igualdad cierta para todo n.
Por tanto tenemos que  , como queríamos.
, como queríamos.
Ejercicio 40.
Probar la igualdad 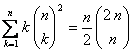
Solución
Podemos expresar la suma como:
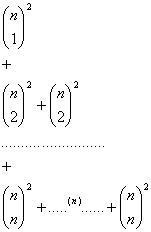
Por tanto, si sumamos por columnas obtenemos 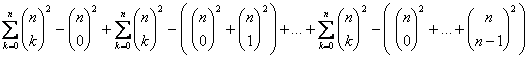
Esto es igual a  . Teniendo en cuenta que
. Teniendo en cuenta que 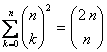 como vimos en el problema previo, tenemos que esta última expresión es igual a
como vimos en el problema previo, tenemos que esta última expresión es igual a  . Haciendo el cambio de variable
. Haciendo el cambio de variable ![]() y aplicando la identidad
y aplicando la identidad ![]() , vemos que esta última expresión es igual a
, vemos que esta última expresión es igual a  .
.
Tenemos por tanto la siguiente igualdad: 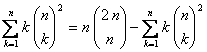 , que implica
, que implica 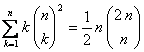 , como deseábamos.
, como deseábamos.