Ejercicio 41 

Supongamos que todo elemento x en un anillo finito R es idempotente, probar que R tiene identidad multiplicativa.  (Propuesto por José Luís Díaz Barrero)

Solución

Como R es finito, lo podemos expresar como . Supongamos que  no tiene identidad multiplicativa, entonces para todo i, existe un  tal que . Pero, como  es idempotente, tenemos que  , por lo que la función   no es inyectiva, y entonces  es un divisor del 0:

En otro caso, , por lo que   es inyectiva, contradicción. Por tanto, todos los elementos de  son divisores del 0.

Por otro lado, tenemos que para todo ,

(La última igualdad es porque   es idempotente). Pero como  es también idempotente, tenemos que . Esto implica que , luego  tiene característica 2, y entonces todo subanillo no trivial de  tiene cardinal par.

Ahora, para todo   consideramos el siguiente conjunto: . Como vimos antes, es un  subanillo no trivial de , por lo que tiene cardinal par. Entonces, si definimos la relación S sobre ,  si , tenemos que existe un número impar de elementos   en  tales que , por lo que los vértices del grafo asociado a  tienen grado impar, pero esto es imposible ya que el grafo tiene un número impar de vértices. Por tanto,  tiene una identidad multiplicativa. (El número de vértices de grado impar en un grafo no dirigido ha de ser par. Obsérvese que el grafo de  es no dirigido ya que  es simétrica, porque  es abeliano: para todo i, j, y entonces  . Por tanto, )

Ejercicio 42.

Sean ,  matrices cuadradas de orden n. Probar que ,  donde las matrices ,  se obtienen de ,  intercambiando sus respectivas primera y k-ésima columna.

(Propuesto por José Luís Díaz Barrero)

Solución

Tenemos que  , , por lo que  , , y entonces

Por otro lado, si  tenemos que  ,  (ya que  ,  se obtienen de ,  intercambiando dos columnas), por lo que:

, y  entonces , como queríamos ver.

Ejercicio 43.

Sea  una sucesión de términos positivos,

a) Demostrar que

b) Demostrar que si  es divergente, entonces  es divergente (indicación: utilizar el apartado a)

(Propuesto en la Universidad Carlos III, titulación de ingeniería de telecomunicaciones)

Solución

a) Como  es una sucesión de términos positivos,  es creciente en , por lo que

b) Si llamamos  a la sucesión de sumas parciales de , la parte izquierda de la desigualdad demostrada en a) es . Entonces, si  convergiera a , sería , por lo que . Pero entonces aplicando la desigualdad demostrada en a) tenemos que 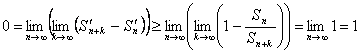, contradicción (en la segunda igualdad hemos utilizado que  es divergente, por lo que . Por tanto, al ser  una serie de términos positivos no convergente, será divergente.